Números Random

[http://imgs.xkcd.com/comics/random_number.png]

Discusión:

En ésta entrada, discutiremos la imagen anterior, donde al principio al verla se nos hará un poco raro si no estamos acostumbrados a la aleatoriedad.

Siendo un poco geeks muchas veces dedicamos tiempo haciendo funciones o buscando como hacer un algoritmo o complementado uno, para garantizar que estamos obteniendo un número aleatorio, muchas veces lo que se tiene es una frecuencia, pero ésta se va repitiendo siendo no aleatoria, así que lo que se hace es alargar la frecuencia y así hacerlo un poco mas aleatorio.

Ya volviendo un poco a la imagen no sabemos que es el valor que nos regresará, más que probabilidades de cuál podría ser el número.

En la imagen podemos ver que al momento de ser llamada la función nos regresara siempre el 4, pero como se comento, no podemos determinar si es aleatorio, ya que puede regresarse cualquier valor.

Ya finalizando des dejo otra imagen que saque de random.org donde podemos encontrarnos con el mismo problema, donde puede que haya visto número aleatorios anteriormente y al momento de dar el valor se menciona nuevamente el mismo número.

[http://www.random.org/analysis/dilbert.jpg]

Referencia:

http://xkcd.com/221/

http://www.random.org/analysis/dilbert.jpg

laboratorio 7: Automatización

Para ésta entrada escogí el problema P 9.2, el cuál consiste en sacar los diagramas de nyquist y sus margenes.

Funciones:

Para realizar éste problema utilicé la las funciones que nos proporciona octave las cuales son la de nyquist que nos devuelve su diagrama y margin.

Reporte Proyecto Final: Control de velocidad de un motor de corriente directa

Proyecto:

"Control de velocidad de un motor de corriente directa"

Introducción:

Existen diversas situaciones donde el control de la velocidad de un motor es crítica, por ejemplo, cuando un robot es movido por 2 motores y se quiere avanzar en cierta dirección, controlar la velocidad de ambos es importante. La velocidad de rotación de un disco duro o un lector de CD/DVD es otro caso. Para ello es necesario adaptar el motor a diversas situaciones de funcionamiento que puedan suceder, por ejemplo, si un móvil va cuesta arriba o cuesta abajo, o cuando existe fricción entre las partes.

Funcionamiento General:
Principalmente el proyecto esta constituido por 3 partes:

• Sensor: Que consta de un optointerruptor ITR8102 y un disco horadado como encoder.
• Microcontrolador: El cual es un Arduino UNO que procesa la salida del sensor para adaptar la velocidad.
• Planta: Será el motor eléctrico el cual será controlado.

Laboratorio 6 de Automatización

Para ésta entrada, me toco obtener la controlabilidad y observabiliad del sistema dado:

Respuesta:

Desarrollo:
Para obtener la observabilidad y controlabilidad del sistema se empleo octave usando la librería de control, con la función de ctrb, obsv y una vez tenidas éstas, emplear la función det, que te de su determinante.

Nota:
Otra de las formas para obtener ésto, es empleando la fórmula respectiva de cada una:

Donde la primera es la de controlabilidad y la segunda de observabilidad.

Cñódigo en Octave

Salidas:

Conclusiones
Donde podemos observar que la salida proporcionada de control y observabilidad da como salida 14 y 5, siendo el sistema completamente controlable ya que mensiona el teorema que este tiene un rango máximo y nuestra salida es dirente a cero, siendo ésto aceptable y el sistema es del todo observable ya que su salida es 5 y en el teorema mensiona que debe de ser diferente a cero.

Referencias:
http://es.wikipedia.org/wiki/Controlabilidad
http://es.wikipedia.org/wiki/Observabilidad

Reporte grupal Automatización

El reporte grupal de esta semana se encuentra en el blog de mi compañero Juan Carlos

El equipo esta conformado por:
Juan Carlos
Rafael

Lectura Científica

Titulo:

"Optimal Estimation of Position and Heading for Mobile RobotsUsing Ultrasonic Beacons and Dead-reckoning".

Descripción:

Este tipo de control es utilizado para el posicionamiento y determinación en ángulo de un robot, cuando se encuentra que las ruedas del robot son imperfectas o se deslizan mucho, causando que se genere errores en la determinación de su posición.

Respuesta:
El artículo mensiona una solución al problema, usando guías ultrasónicos para saber su posición correcta, mejorando lo adaptativo del robot y sus actividades autónomas.

La estructura usada, para la resolución del problema fue usar 6 balizas(emisor de señal) ultrasónicos conectados a un control de transmisión, un receptor compuesto por 8 sensores ultrasónicos (receptores), tomando las señales de las balizas para sacar la estimación de posición  y orientación usando el filtro de Kalman, donde éste estima el estado de n dimensional de un sistema denotado por x, dado un conjunto de m dimensiones del vector y. El estado para localizarlo contiene la posición, orientación y velocidad del robot.
El filtro de Kalman ayuda a éste a encontrar el estado oculto de un sistema dinámico lineal, cuando se tiene diferentes valores de señal en tiempos diferentes (siendo éstos las emisiones y  recepciones de las balizas).

Donde aplica el control:
El control aplica, al momento de su retroalimentación, ya que las balizas mandan una señal y los receptores calculan los errores de posición, obteniendo así la retroalimentacón que será utilizada, ya sea para emitir su posición correcta actual, corregir su posición, o entre otras que éste destinada a ralizar

Ejemplos de posibles usos:
Principalmente en los carros  autónomos manejando ésto en zonas más grandes, como el prototipo del carro de google, carritos exploradores, etc.

Opinión:
Este tipo de control en lo personal me podría ayudar, ya que en proyectos anteriores buscaba controlar un carrito, pequeños robots o drones en una determinada zona, mejorando la transición que seguiria el robot, como pasar algunos obstáculos.

Desventajas:
Algunas de las  desventajas que encontré fue que no muchas veces se buscará una zona determinada, así que depende mucho de las balizas y que éstas al ponerlas en zonas mas grandes el tiempo de transmisión o recepción aumentaría, otra de ellas fue que hoy en día varios sistemas o robots móviles emplean sensores lasers para  su correcta calibración o como guía de posicionamiento, siendo esto más exacto y más rapido.

Referencia:
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=220053

Tarea 5: Dibujar el diagrama de Bode

Para ésta entrada, me tocó realizar el diagrama de bode de la siguiente función:

Desarrollo:

Así que lo buscado será primero simplificar, para hacerlo más fácil.

 Una vez tenido el polinonio es multiplicado por 30.3215

Ahora tenemos el num. y den.

Una vez que se obtiene ésto es mas fácil graficarlo con octave ya que tiene una función propia

Código:

num = [30.3215 39.41795 12.81083];
den = [0 1 0];
s1 = tf(den, num)
bode(s1)

Salida:

Estabilidad de nuestro programa

Para ésta entrada, se nos pidió, hacer pruebas en nuestra función de transferencia y determinar si ésta es o no es estable.

Función de transferencia:

Diagrama de bode & nyquist:
El diagrama de bode y nyquist, nos servirá para determinar en forma gráfica que tan estable o inestable es, como se menciono con anterioridad, si en nuestro plano, observamos que va a la derecha, nuestro sistema es inestable, caso contrario si tiende a la izquierda.

Imagen diagrama de impulso:
El impulso, nos sirve de otra forma gráfica para determinar que tan estable o inestable es nuestro sistema, ya que dependiendo del impulso que se le de nos mostrará como se va comportando en forma de onda.

Código:

function estabilidad%(num, den)
k = 1;
v = 2.5;
num = [k v];
den = [3 4 1 434]; #Este ultimo es la constante de distancia del sensor determ.objeto
sys = tf(num, den)
figure (1)
nyquist (sys)
figure (2)
rlocus (sys)
figure (3)
impulse (sys)
raices = roots (den)

contador = 0
for i = 1:length(raices)
if real(raices(i)) > 0
contador + 1; 
endif
endfor

if contador > 0
printf("Sistema Inestable")
else printf("Sistema Estable \n")
endif

endfunction

Salidas:

duda

duda

duda

Conclusiones:
En las salidas mostradas, se puede ver en las gráficas de nyquist es semi-estable, ya que hasta cierto punto la gráfica se queda en el semiplano de la izquierda.


Notas:
La función de transferencia empleada, fue convertida a ecuación lineal, para pasarla a numerador y denominador, aunque se necesitan otras pruebas para verificar su correcta converción.


Referencia:
http://octave-online.blogspot.mx/2010/05/impulse.html
http://es.wikipedia.org/wiki/Teorema_de_Routh-Hurwitz
http://www.slideshare.net/tonivi99/sistemas-de-control

Tarea 4: Laboratorio Automatización

Para ésta entrada se nos encargo realizar el problema 6.1, en la cuál me piden dibuar el siguiente sistema:

Teniendo la función de transferencia, ponemos nuestro angulo de condición:

Donde (K(s+1))-s^2 puede ser sustituido por la siguiente ecuación:

Una vez obtenido éste sustituimos todas las s, por δ + jw.

El libro nos mensiona que δ + jw, puede ser sustituido por tan^-1, asi que sustituyendo lo anterior y quitando el 2, para reordenarlo obtenemos:

Podemos reducir la ecuación anterior agregando tan a ambos lados, para despues quitar y asi tener w/δ, reducido .

Igualamos a cero la ecuación, para poder llegar a w/δ y así simplificar valores iguales:

Apoyandome con el libro, mensionan que podemos sustituir por lo siguiente:

donde obtenemos:

Teniendo ésta ecuacion, podemos igualar a cero teniendo lo siguiente:

Teniendo ésta ecuación seguimos a graficarla, donde w = 0, es nuetro eje de los reales de s = - 1 a s = infinito, nuestra segunda ecuación es la ecuación de nuestro circulo donde el centro es δ = -1, w = 0 y el radio es igual a 1 

Referencias:
http://autoycontrolave.blogspot.mx/ 
 Libro de Modern Control Engineering, Fourth Edition, de Katsuhiko Ogata
http://www.google.com.mx/url?sa=t&rct=j&q=&esrc=s&source=web&cd=7&ved=0CD4QFjAG&url=http%3A%2F%2Fes.scribd.com%2Fdoc%2F19150402%2FLazo-Abierto-y-Cerrado&ei=I26AUIrVPKSC4gSEx4CYAQ&usg=AFQjCNEc8ICl6bn7EJuJRZDLTmFOUA6a2Q&sig2=PmbObgDAPms1dbXhN9xlJA&cad=rja

Reporte 2: Diagrama de Bloques

Para ésta entrada, lo buscado será realizar un diagrama de bloques de la función de transferencia obtenida del proyecto.

Función de transferencia:
Para mi función de transferencia es el de un sistema de abrir y cerrar un cerrojo de una puerta, dependiendo de un sensor ultrasónico(La persona se encuentra cerca de la puerta), éste es mi entrada y como salida, da el movimiento del servomotor.

Video proyecto anterior:
 
Función de Transferencia:

Más abajo dejaré explicada de como saque mi función de transferencia, que fue lo que me quedo pendiente del reporte anterior.

Donde (TmS+1) y Km  ésta denonata por el servomotor(velocidad del servo, flujo angular, inercia y fricción), debo de mencionar que ésta ecuación de la función del servomotor la saque de un libro mencionado de las referencias.

stD(s))  y 2, esta denotado por la función del sensor ultrasónico

Nota: Explicación mas profunda en otra entrada.

Diagrama de Bloques

Ayuda:

Traducido ésto en diagrama de bloques queda dado por la siguiente imagen, si quieren más información de como pasar  la función de transferencia en diagrama de bloques pueden visitar ésta liga.

Referencias:
http://www.scribd.com/doc/39580374/Modelo-Matematico-de-Sistemas-Dinamicos
https://docs.google.com/viewer?a=v&q=cache:le0jciU-XBYJ:gama.fime.uanl.mx/~agarcia/materias/ingco/apclas/03%2520-%2520Diagramas%2520de%2520Bloques.pdf+&hl=es&gl=mx&pid=bl&srcid=ADGEESg40f8PkHfRFcKXh3_Y1aCYLpbCp7v1gXrVUNlT7VMhf7BP481V4CHKA2eWdtVB2lStVGyhlIgMs5pmoYm-Hgx9XXPZqHoKpdnET2JL-WTjfR_3Bzya1b2AdLBbX2qyY9uyzLxa&sig=AHIEtbQ6s9vfCg_r40E8t47kfA1zgKpOXg

Tarea 3: Laboratorio de Automarización MAtriz de tranferencia

Para ésta entrada, se me encargo realizar la actividad de encontrarr la matriz de transferenciade l siguiente sistema:

Solución:

Referencia:
http://www.wikimatematica.org/index.php?title=Matrices_de:_Transferencia,_Transici%C3%B3n_de_Estados_y_Modal
http://delta.cs.cinvestav.mx/~mcintosh/comun/jesus/node10.html

Tarea 2 laboratorio: Transformada de Laplace

Para ésta entrada, se encargo realizar un problema el cuál consistía en sacar la Transformada de Laplace del siguiente problema:

Procedimiento:

Para realizar el problema propuesto, lo que se realizó fue separarla y una vez teniendo sus resultados, multiplicarlos.

Procesimiento primero:

Procedimiento segundo:

Así que teniendo los resultados de éstos, nos dará:

Referencias:
http://html.rincondelvago.com/transformada-de-laplace.html
Ayuda Avendaño

Controladores Industriales (puntos extra)

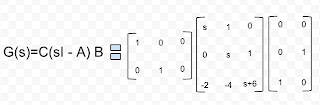
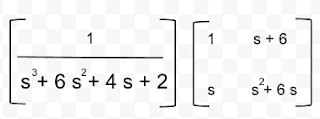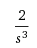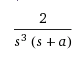Para ésta entrada veremos algunos tipos de controladores, pero antes un controlador lo ocupamos en automatización donde comparamos el valor de salida de la planta(nuestro sistema) con el valor deseado, determinando su desviación(podríamos mencionarlo como error) y produciendo una señal de control que reduce ésta desviación. 

http://www.sapiensman.com/control_automatico/#funcion_del_control_automatico

Expresándolo un poco más sencillo es donde buscamos mantener regulados determinados valores deseados, para garantizar la seguridad y estabilidad de la planta o sistema. 

Un ejemplo que podríamos mencionar es el sistemas de los minisplits, donde nosotros damos la temperatura esperada y ésta buscará que la habitación llegue a ella.

Para ésto se requiere del acoplamiento, que es un mecánismo de trasmición y de medición (transmisor/sensor), que emplearemos como acción correctiva(control)

Los tipos de controladores que veremos son los siguientes:

• De dos posiciones o controladores on-off
• Control proporcional integral.
• Control proporcional derivativos.
• Control proporcional integral-derivativo.

Diferencias y ejemplos de los diferentes controladores:

Controladores on-off: Éste sistema como su nombre lo indica sólo tiene dos posiciones fijas y lo podemos encontrar fácilmente en aquellos sistemas donde empleen una acción booleana, el encendido y el apagado. Éste tipo de controlador es sencillo y bárato, así que es muy usado tanto en la industria como dómesticos.

Ejemplo:
Algunos ejemplos a mencionar, podrían ser el encendido y apagado de un sistema, luces, controladores de abrir y cerrar válvulas, entre otras.

http://www.emi-mexico.com/imgs/int/valvulas/images/port_valvulas.jpg

Control proporcional integral (PI): A éste tipo de control a la salida se le suma la acción integral, que la corrige tomando en cuenta la magnitud del error(retroalimentación) y el tiempo que este ha permanecido en el. Para ello se le programa al control una constante(que nosotros la tomaremos como I), donde I es la cantidad de veces que aumenta la acción proporcional por segundo. La salida se corrige en una cantidad equivalente a la integral del error multiplicada por I. O dicho en otras palabras, cada error producido en cada segundo, lo vamos agregando en una variable y una vez que el sistema sobrepasa determinado umbral, en ésta le vamos ir reduciendo los valores guardados para que el sistema se mantenga estable.

Ejemplo:

Un ejemplo a mencionar, podría ser el sistema de enfriado de los refrigeradores que llevan los trailers que transportan productos, donden necesitan estar en una determinada temperatura para que se conserven.Éste tipo de controlador como ya se mencionó , buscará que al pasar determinado umbral irlo regulando.

http://images01.mundoanuncio.com/ui/3/50/14/l-1226524614-01.jpg

Control proporcional derivativo (PD): A éste tipo de control, le agregamos la capacidad de considerar también la velocidad de la variable en el tiempo. Éste tipo de control nos ayuda adelantar la acción de control del mando de salida para obtener así un una planta más estable. 

Ejemplo:

Un ejemplo a mencionar, podría ser en sistemas de regulación de calderas, donde buscaremos adelantar nuestro valor(temperatura) para regularlo, por ejemplo cuando éste va subiendo o bajando rápidamente y ésta a punto de pasar determinado umbral(valor esperado) en un determinado tiempo, lo que haremos es subir o bajar los calefactores, para estabilizar su temperatura.

http://www.elprisma.com/apuntes/ingenieria_industrial/tiposdecalderasindustriales/background4.jpg

Control proporcional integral-derivativo (PID): Este tipo de control como su nombre lo dice es la combinación de los dos anteriores mencionados, la ventaja de éste es que se busca lo óptimo, ya sea en PI o PD y la mala es que encontrar el óptimo puede darnos un proceso largo, ya que solo un conjunto de éstos valores lodará. Éste tipo de control es muy usado para manejar o controlar sistemas de presion, flujo, fuerza, velocidad(empleados en la química en su mayoría).

Ejemplo:

Unos de los ejemplos o aplicaciones más prácticas son los reguladores de velocidad en los cruceros, reguladores de presion en un determinado tanque, satélite, naves espaciales o aviones, donde en éstos últimos se busca regular la presión atmosférica.

http://www.cnnexpansion.com/media/2010/03/01/satelite.jpg

A continuación les dejo unas gráficas donde muestra el comportamiento de diferentes controladores, donde podemos notar que en el proporcional integral, se muestra más inéstable y la proporcional integral-derivativa, se encuentra más estable.

Referencia:

http://es.wikipedia.org/wiki/Proporcional_integral_derivativo
www.scribd.com/doc/37267444/Tutorial-Control-PI
http://www.scribd.com/doc/73745129/17/CONTROL-PROPORCIONAL-INTEGRAL-PI
http://www.scribd.com/doc/17702998/Tipos-de-Controladores
http://kush-tripathi.blogspot.mx/2009/12/control-system-is-device-or-set-of.html