[http://imgs.xkcd.com/comics/random_number.png]
Discusión:
En ésta entrada, discutiremos la imagen anterior, donde al principio al verla se nos hará un poco raro si no estamos acostumbrados a la aleatoriedad.
Siendo un poco geeks muchas veces dedicamos tiempo haciendo funciones o buscando como hacer un algoritmo o complementado uno, para garantizar que estamos obteniendo un número aleatorio, muchas veces lo que se tiene es una frecuencia, pero ésta se va repitiendo siendo no aleatoria, así que lo que se hace es alargar la frecuencia y así hacerlo un poco mas aleatorio.
Ya volviendo un poco a la imagen no sabemos que es el valor que nos regresará, más que probabilidades de cuál podría ser el número.
En la imagen podemos ver que al momento de ser llamada la función nos regresara siempre el 4, pero como se comento, no podemos determinar si es aleatorio, ya que puede regresarse cualquier valor.
Ya finalizando des dejo otra imagen que saque de random.org donde podemos encontrarnos con el mismo problema, donde puede que haya visto número aleatorios anteriormente y al momento de dar el valor se menciona nuevamente el mismo número.
[http://www.random.org/analysis/dilbert.jpg]
Referencia:


+16.25.34.png)























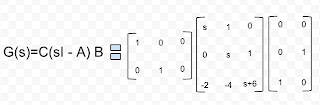

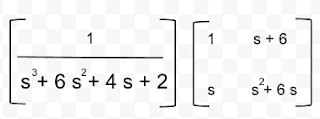







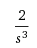
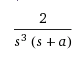

.jpg)